Длина окружности формула
92
Что скрывается за формулой длины окружности

** изображение создано или обработано с помощью ИИ.
Начнём с основы. Окружность — это линия, у которой все точки находятся на одинаковом расстоянии от центра. Это расстояние называется радиусом. Длину окружности обычно обозначают буквой L.
Самая используемая формула выглядит так: L = 2πR, где R — радиус, а π ≈ 3,14. Если вместо радиуса дан диаметр, формула меняется на L = πD. По сути, это одно и то же, потому что диаметр в два раза больше радиуса.
Важно не просто выучить, а понимать, что она считает. Длина окружности — это путь по краю круга. Например, сколько «проезжает» точка на колесе велосипеда за один оборот или какой длинны край у крышки от бутылки. Как только ты подставляешь реальные размеры, формула перестает быть абстрактной, начинает работать как инструмент.
Если ты умеешь находить длину окружности, то уже можешь проверять расчеты, прикидывать размеры, понимать, откуда берутся числа. Для 7 класса этого достаточно, чтобы уверенно решать задачи, не путаться в обозначениях.
Почему π — не просто мем из интернета

** изображение создано или обработано с помощью ИИ.
Число π появляется не случайно и не «по договорённости». Еще в древности заметили: если длину любой окружности разделить на её диаметр, результат почти не меняется. Большой круг или маленький — отношение одно и то же. Именно это постоянство и назвали π.
Его знали задолго до современных формул: в Древнем Египте и Вавилоне уже пользовались приближенными значениями. Сегодня мы знаем, что π — бесконечная дробь, у которой нет конца и повторяющегося периода. Поэтому точного значения не существует, его нельзя полностью записать ни на бумаге, ни в компьютере.
Но для задач 7 класса и для реальных расчетов это не проблема. Обычно берут π ≈ 3,14. Иногда — 3,1416, если нужна большая точность. Этого хватает и в школе, и в технике. Подставлять десятки знаков после запятой нет смысла: результат от этого принципиально не изменится.
Важно не количество цифр, а понимание идеи. π — это связь между длиной окружности и её диаметром. Если ты это понял, значит, число π для тебя не загадка, а рабочий инструмент.
Практическое применение и неожиданные примеры

** изображение создано или обработано с помощью ИИ.
Формула нужна не только в школе. Она пригодится, когда проектируют механизмы, рассчитывают путь роботов или планируют дизайн объектов. Например, я как-то помог другу узнать, сколько светодиодов нужно для подсветки круглого зеркала.
Измерили радиус, подставили в L = 2πR, и получилось идеально — экономия материалов и времени налицо. Попробуйте мысленно посчитать длину обода колеса — сразу видно, как универсальна она.
Можно ли обойтись без формулы? Теоретически — да: просто обмотай окружность верёвкой и измерь длину линейкой. Но это подходит только для уже существующих предметов и дает приближенный результат. А если нужно рассчитать длину колеса будущего велосипеда до его изготовления, без формулы не обойтись.
Особенно когда работаешь в инженерном проекте или учишься в онлайн-школе с курсами подготовки для 7 класса. Там формулы становятся надежным помощником в решении задач.
Частые ошибки при использовании формулы

** изображение создано или обработано с помощью ИИ.
Ошибки при работе встречаются чаще, чем кажется. Вот на что особенно стоит обратить внимание:
- Путают радиус и диаметр. Диаметр в два раза больше радиуса, и формула меняется: L = 2πR или L = πD.
- Забывают про единицы измерения. Если радиус в сантиметрах, длина тоже получится в сантиметрах.
- Слишком точное π для простых задач. В школе достаточно π ≈ 3,14; лишние цифры не дают практической пользы.
- Неправильно умножают. Иногда при использовании радиуса забывают умножить на 2, и длина получается вдвое меньше.
Если контролировать эти моменты, ошибки почти исчезают. Главный совет: не заучивай формулу как набор букв, а пойми, что она считает. Понимание — лучший способ не ошибиться, уверенно решать любые задачи.
Полезные приёмы, лайфхаки и мини-инструкции
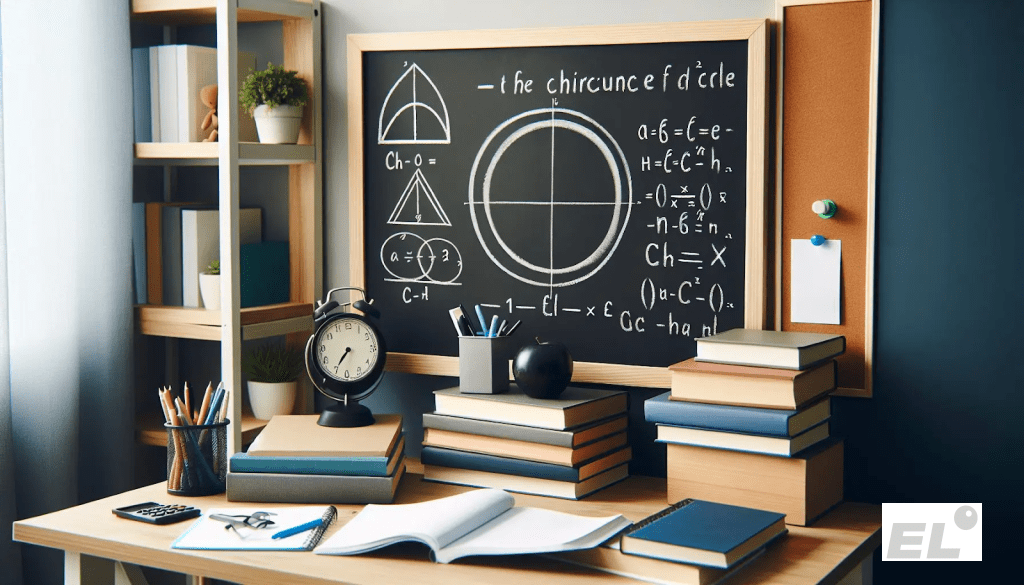
** изображение создано или обработано с помощью ИИ.
Вот простой чек-лист, который помогает не ошибиться:
- Определи, что дано — радиус или диаметр.
- Выбери нужную формулу: L = 2πR для радиуса или L = πD для диаметра.
- Подставь значение π с подходящей точностью (для школы обычно 3,14).
- Посчитай длину, не забывая про единицы измерения.
- Проверь результат — логически и арифметически.
Если длина кажется странной, например, меньше диаметра, то проверь порядок действий. Часто ошибки случаются не в формулах, а из-за невнимательности при вводе чисел в калькулятор. Мысленно сравни результат с реальным размером: радиус 5 см не может дать длину окружности 10 см. Такой здравый смысл помогает ловить промахи быстрее любых проверок.
Ответы на популярные вопросы о длине окружности

** изображение создано или обработано с помощью ИИ.
Вопрос: Нужно ли помнить обе формулы? Ответ: достаточно одной. Если известен радиус, берём L = 2πR, если диаметр — L = πD.
Вопрос: Почему в задачах используют разные значения π? Ответ: всё зависит от точности. В школе хватает 3,14, а в инженерных расчётах используют 3,1416 или больше.
Вопрос: Можно ли применить эту формулу к эллипсу? Ответ: нет. У эллипса нет одного радиуса, он «растянут», длину считают по более сложной формуле, которую изучишь позже.
Вопрос: Что делать без калькулятора? Ответ: использовать приближения. Например, при радиусе 10 см длина окружности ≈ 2 × 3,14 × 10 = 62,8 см.
Немного практики помогает понять формулу на деле. Возьми монету, измерь диаметр и умножь на π — получишь длину окружности. Проверь результат шнурком или линейкой, совпадает! Такие простые действия делают математику наглядной.
И если когда-то путался в словах «радиус» и «диаметр», не переживай. Главное, чтобы формула длины окружности стала не просто в памяти, а интуитивно понятной. Она пригодится: хоть для расчёта колеса велосипеда, хоть для будущего проекта, который ты придумаешь за кружкой кофе.

Хочешь начать готовиться, но остались вопросы?
Заполни форму, и мы подробно объясним, как устроена подготовка к ЕГЭ и ОГЭ в ЕГЭLAND













