Формула квадрата суммы

Откуда берется формула и зачем нам этот квадрат

** изображение создано или обработано с помощью ИИ.

Давай разберем квадрат суммы на деле. Формула (a + b)² = a² + 2ab + b² — это не просто строчка в учебнике, а результат обычного умножения скобки на саму себя.

Работает это так: ты умножаешь каждое слагаемое из первой скобки на каждое слагаемое из второй. Получается: a * a = a², a * b = ab, b * a = ab, b * b = b². Потом складываешь: a² + ab + ab + b² = a² + 2ab + b².

Например, (3x + 5)². Здесь a = 3x, b = 5. Следуем шагам: квадрат первого: (3x)² = 9x². Удвоенное произведение: 2 * 3x * 5 = 30x. Квадрат второго: 5² = 25. Итог: 9x² + 30x + 25.

Не пытайся вызубрить — пойми эту последовательность. Она понадобится тебе постоянно: чтобы раскрывать скобки, упрощать большие выражения и даже в некоторых задачах по геометрии, физике. Когда видишь подобную конструкцию, просто определи, что играет роль a, что b, действуй по плану. Это станет твоим надежным инструментом.

Как не запутаться в скобках и знаках

Смотри, главная ловушка с квадратом суммы — это пропустить удвоенное произведение. Многие думают, что (a + b)² — это просто a² + b². Но это не так. Между ними всегда есть 2ab, и без него формула не работает. Это самое важное.

Чтобы не ошибиться, не полагайся на память, а делай шаги. Просто умножь скобку (a + b) на саму себя, как обычно: (a + b) * (a + b) = aа + ab + ba + bb = a² + ab + ab + b² = a² + 2ab + b².

Теперь про знаки. Если перед скобкой минус, например (-a + b)², ничего сложного. Просто считай, что твое первое слагаемое — это (-a), а второе b. Тогда:

• Квадрат первого: (-a)² = a² (минус исчезает, потому что квадрат).
  
• Удвоенное произведение: 2 * (-a) * b = -2ab.
  
• Квадрат второго: b².
  
• В итоге: a² – 2ab + b².

Не путай эту формулу с квадратом разности (a – b)², где будет a² — 2ab + b². Разница в знаке внутри скобки, и он точно переходит в знак перед 2ab.

Потренируйся на простом примере: (2x — 3)². Первое слагаемое (a) = 2x, второе (b) = 3, но в скобках минус. Пишем: (2x)² — 2 * (2x) * 3 + 3² = 4x² — 12x + 9.

Действуй так всегда: найди a и b, определи знак, а потом аккуратно выпиши три слагаемых. Со временем будешь делать это на автомате, но сначала только так, по шагам.

** изображение создано или обработано с помощью ИИ.

Наглядное понимание через геометрию

** изображение создано или обработано с помощью ИИ.

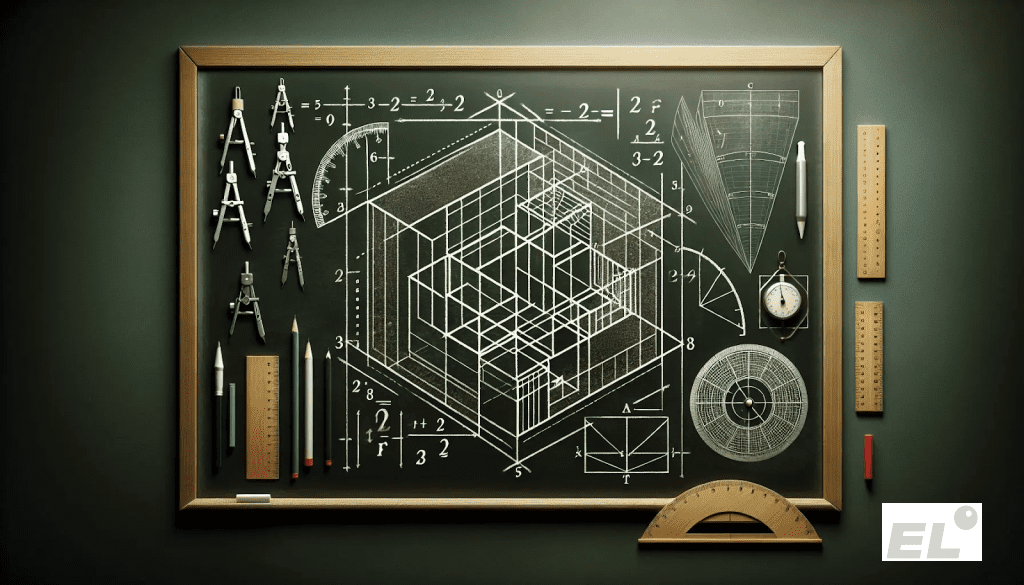
Давай нарисуем квадрат, чтобы увидеть формулу вживую.

Представь квадрат со стороной (a + b). Проведи внутри него две линии: одну на расстоянии a от левого края, другую на расстоянии a от верхнего края. У тебя получится четыре фигуры.

• В левом верхнем углу — квадрат со стороной a. Его площадь: a².

• В правом нижнем углу — квадрат со стороной b. Его площадь: b².

• Оставшиеся два прямоугольника: один сверху справа, другой снизу слева. У каждого длина a, ширина b. Площадь каждого — a * b. А их два, поэтому их общая площадь: 2ab.

Теперь посмотри: площадь всего большого квадрата равна сумме площадей всех частей: a² + ab + ab + b² = a² + 2ab + b².

Это и есть (a + b)², только показано наглядно. 

Формула перестает быть сухим правилом, ты видишь, откуда берётся каждое слагаемое. Попробуй сам это набросать на листочке. Когда соединишь алгебру с геометрией, понимание станет намного глубже.

Практика решает всё: от простого к сложному

** изображение создано или обработано с помощью ИИ.

Давай проверим на практике, как это работает. Возьмем примеры:

• (2x + 3)². Здесь a = 2x, b = 3; a² = (2x)² = 4x²; 2ab = 2 * 2x * 3 = 12x; b² = 3² = 9. Итог: 4x² + 12x + 9.

• (x + 7y)². Здесь a = x, b = 7y; a² = x²; 2ab = 2 * x * 7y = 14xy; b² = (7y)² = 49y². Итог: x² + 14xy + 49y².

Попробуй теперь обратное действие — увидеть формулу в выражении. Например, выражение x² + 8x + 16. Спроси себя:

• Первое слагаемое — квадрат чего? Квадрат x.

• Последнее слагаемое — квадрат чего? Квадрат 4 (потому что 4² = 16).

• А средний член — это удвоенное произведение? Проверяем: 2 * x * 4 = 8x. Да, точно совпадает.

• Значит, это и есть (x + 4)².

Как закрепить? Сделай так: реши 3-4 примера на раскрытие скобок. Потом найди 3-4 квадрата в уже готовых выражениях (как x² + 8x + 16). Эти две стороны одной медали: раскрытие и сворачивание, научат тебя видеть формулу в любом виде. Делай это без спешки, проверяя каждый шаг. Скоро ты станешь узнавать её с первого взгляда.

Советую заглянуть в онлайн школу https://el-ed.ru/, где есть курсы подготовки для 8 класса. Там формулы подаются не зубрежкой, а через понимание. А при желании можно пройти пробные задания, увидеть пояснения и даже задать вопросы преподавателям.

Типичные ошибки и лайфхаки от практика

** изображение создано или обработано с помощью ИИ.

Давай соберём всё в простые, но железные правила. Они помогут тебе не спотыкаться.

• Не трогай скобки, пока не посмотришь на степень. Сначала полностью разберись, что у тебя внутри скобок (особенно если там минус), и только потом возводим в квадрат. Потому что (-a + b)² и -(a + b)² — это разные вещи.

• Следи за знаком как за самым ценным. Когда возводишь в квадрат выражение с минусом, например (-x + 5)², квадрат первого слагаемого (-x)² даст +x², а вот в удвоенном произведении знак останется: 2 * (-x) * 5 = -10x.

• Не ленись делать черновик. Выписывай шаги: сначала a², потом 2ab, потом b². Потом сложи. Эти десять секунд спасают от случайной ошибки в контрольной, когда нервничаешь.

• Не сворачивай путь в уме. Сделай всё по правилам, даже если пример кажется простым. Механика важна: она доводит действие до автоматизма, и потом ты сможешь делать это быстро, но безошибочно.

• Проговаривай про себя. Говори: «Квадрат первого… плюс удвоенное произведение… плюс квадрат второго». Это помогает удержать структуру и не потерять среднее слагаемое.

Попробуй на таком примере с подвохом: (-3x + 2)². Не спеши. Определи: a = (-3x), b = 2; a² = (-3x)² = 9x²; 2ab = 2 * (-3x) * 2 = -12x; b² = 2² = 4. Итог: 9x² — 12x + 4.

Когда сделаешь так несколько раз, формула станет твоим надежным инструментом. А скорость придет сама собой, через практику, а не через спешку.

Как проверить, что ты действительно понял

** изображение создано или обработано с помощью ИИ.

Сначала придумай свои примеры и реши их, а потом проверь, раскрыв скобки обратно. Потом попробуй объяснить правило кому-нибудь другому. Если сможешь донести просто, значит, сам во всём разобрался. Наконец, научись видеть формулу в готовом виде: например, выражение x² + 6x + 9 — это замаскированный квадрат (x + 3)². 

А теперь главный вопрос. Почему в середине формулы 2ab, а не просто ab? Всё просто. Когда перемножаются скобки (a + b)(a + b), слагаемое ab появляется два раза. Сначала a умножается на b, потом b умножается на a. Эти два одинаковых слагаемых ab + ab и дают в сумме 2ab.

Если видишь эту логику, то ты на верном пути. Это понимание — тот самый крепкий кирпич, на котором держатся более сложные темы.