Координаты точки на плоскости

Как вообще появились координаты и зачем они нужны

Система координат — это не просто школьная тема, а фундаментальный язык пространства. Декарт, по сути, создал универсальный способ перевести геометрию (где вещи?) на язык алгебры (как их описать числами.)

Вся суть в соответствии. Каждой точке на плоскости ставится в пару два числа: (x; y). Первое говорит, насколько вправо или влево, второе насколько вверх или вниз. Это гениально просто и невероятно мощно.

Пример с картой, то что надо. Когда ты ищешь кафе, ты не описываешь его словами. Ты смотришь на координаты — пересечение улиц или точку на сетке карты. Всё то же самое: горизонтальная ось (одна улица) и вертикальная (другая улица). Игровой персонаж движется по координатам (x; y), архитектор рассчитывает положение колонны по тем же (x; y).

Это и есть главный прорыв: алгебра и геометрия перестали быть разными предметами. Уравнение y = 2x перестало быть просто строкой. Оно стало прямой линией, которую можно увидеть. Сложную кривую на чертеже стало можно описать точной формулой и исследовать вычислениями.

Поняв это, ты начинаешь видеть координатные системы повсюду: в раскладке мебели в комнате (где поставить стол?), таблице (строка и столбец, твои x и y). Это способ мышления, раскладывать мир на оси и координаты, чтобы сделать его понятным, измеримым, предсказуемым.

Как устроена координатная плоскость

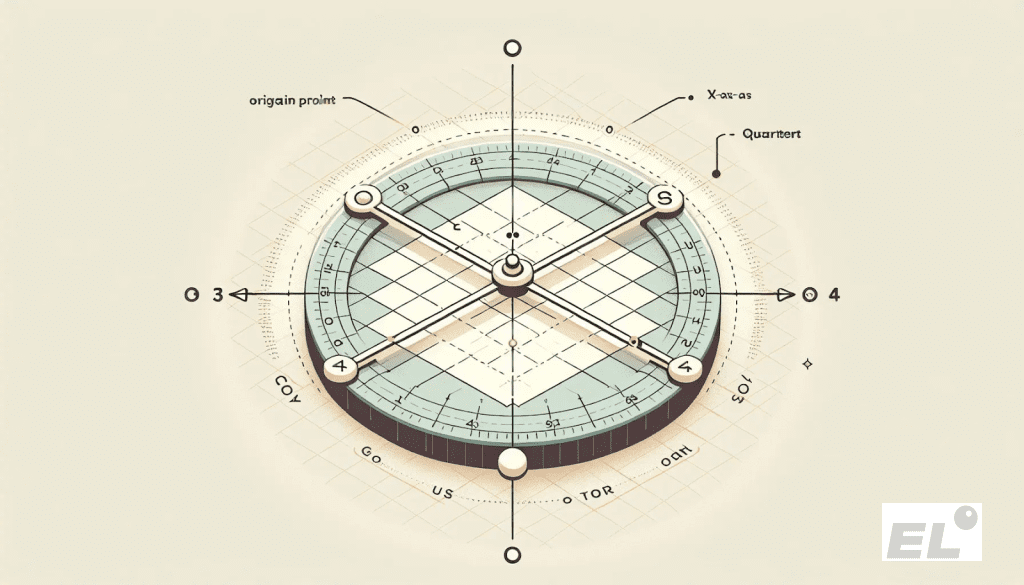
Основа — это пересечение двух перпендикулярных осей. Точка их встречи (0; 0), твой абсолютный центр отсчета, точка отсчета для всех остальных точек.

Разделение на четверти — ключ к пониманию знаков. Простое правило: сначала думай про горизонтали (X), потом про вертикали (Y).

• Право и вверх (+, +) первая четверть. Здесь всё положительно.

• Лево и вверх (-, +) вторая четверть.

• Лево и вниз (-, -) третья.

• Право и вниз (+, -) четвертая.

История с зеркальным графиком — классическая ошибка, которая случается, если перепутать знак у x или y. Если график функции оказался не там, где должен быть, первым делом проверь. Правильно ли ты определил четверть для своих точек.

А насчёт направления осей — важнейший момент. В математике Y растёт вверх. Но в программировании (например, в обработке изображений) ось Y часто направлена вниз, потому что экран сканируется сверху вниз. Это не ошибка, а разные соглашения. Суть не в том, куда смотрит стрелка, а в том, что ты всегда должен знать правила системы, в которой работаешь. 

Если ты понимаешь принцип «одно число — смещение по горизонтали, другое — по вертикали», то сможешь адаптироваться к любой системе координат.

Как находить координаты точки

Координаты точки — это её точный адрес. Чтобы его определить, мысленно проведи от точки перпендикуляр к оси X. Это первое число (например, 3). Затем проведи перпендикуляр к оси Y. Это второе число (например, 2). Адрес записывается в строгом порядке: (3; 2). Путаница возникает, если менять порядок или направление. Запомни: сначала шаг вправо/влево (по X), потом шаг вверх/вниз (по Y).

Составление таблицы для нескольких точек и их построение помогает увидеть закономерность: прямая, парабола, окружность. Это основа для всех задач с графиками. Без уверенного владения этим навыком двигаться дальше бессмысленно. Как рисовать, не умея ставить точку на холсте.

Кстати, если готовишься к экзаменам, освоение координатной системы обязательный шаг. Без этого трудно решать задачи с графиками функций или находить расстояние между точками. Хорошая практика — использовать онлайн-школу с курсами для 8 класса, где ты сразу увидишь, как изменение координат влияет на положение точки. Это поможет закрепить навык не на уровне правил, а на уровне чувства плоскости.

Расстояние между точками и середина отрезка

Когда координаты точек известны, расстояние между ними считается легко и красиво. Для точек A(x₁; y₁) и B(x₂; y₂) формула выглядит так: AB = √[(x₂ − x₁)² + (y₂ − y₁)²].

По сути, это прямое применение теоремы Пифагора. Разность по X и разность по Y — это катеты воображаемого прямоугольного треугольника, а расстояние между точками — гипотенуза. 

Никакой магии, просто чёткая связь между числами и геометрией. И когда это щёлкает в голове, возникает ощущение порядка. Уравнения перестают быть абстракцией, начинают описывать реальные линии в пространстве.

Есть и вторая полезная формула — координаты середины отрезка. Она ещё проще: x = (x₁ + x₂)/2, y = (y₁ + y₂)/2. Это среднее арифметическое по каждой координате. Никаких квадратов, никаких корней, только баланс. 

Я часто говорю ученикам: представьте, что две точки — это два человека, которые хотят встретиться. Середина — это место, куда им идти одинаково далеко. Это компромисс, но честный: никто не уступает больше другого.

Иногда думаешь: а не хватает ли нам в жизни такой же простой формулы для равновесия? Где всё решается не спором, а усреднением позиций. Но даже если в жизни всё сложнее, в математике этот принцип работает безотказно. И именно в таких простых, но глубоких идеях сила координатного метода.

Координаты и практическое применение

Однажды студент спросил: «А зачем вообще знать, где точка находится? Я же не картограф». Вопрос честный, но на деле координаты работают везде, просто часто незаметно.

В компьютерной графике каждая иконка, каждый пиксель имеет свои координаты. В робототехнике — положение манипулятора или дрона задаётся в трёхмерном пространстве. Навигатор определяет местоположение через географические координаты, а приложение знает, куда ты ткнул пальцем, потому что экран тоже координатная плоскость, только с осями, спрятанными за интерфейсом.

Если у человека не формируется это пространственное чувство: где верх, где низ, как двигаться от (0; 0) к (5; –2), то позже ему будет трудно строить графики. И понимать модели, читать схемы, работать с данными. А наверстывать базу, когда вокруг уже сложные темы, долго и нервно.

Кроме того, координаты — это не только про «где», но и про логику. Например: точка внутри треугольника или снаружи? Движется ли объект по прямой или по дуге? Пересекаются ли траектории двух частиц? Всё это решается через координаты.

• В физике: положение тела в пространстве.
  
• В географии: широта и долгота.
  
• В программировании: расположение элементов на экране.

Так что умение читать и записывать координаты — это не школьное упражнение. А универсальный инструмент, который помогает ориентироваться не только на бумаге, но и в реальном мире. И чем раньше он становится привычным, тем свободнее ты чувствуешь себя в любой технической задаче. Даже если никогда не станешь картографом.

Как не запутаться и закрепить навык

Правильный подход — не запоминать, а прочувствовать координатную плоскость. Возьми листок, нарисуй оси и преврати их в свою карту. Пусть точка (2; 3) будет твоим домом, а (-1; 0) остановкой. Так абстракция станет личной и понятной. Сразу увидишь, где какая четверть.

Чтобы не путать оси, присвой им цвета: например, ось X — красная, ось Y — синяя. Ищи координату (5; -2) как маршрут: «5 по красной линии, потом -2 по синей».

Привычка перепроверять — основа. Прежде чем назвать точку, мысленно проведи от неё линии к осям. Верны ли числа? Эта секундная пауза убережет от грубых ошибок.

А чтобы мышление стало гибким, обсуждай задачи с другими. Предлагайте друг другу задачи на движение по координатам. В диалоге понимание приходит быстрее, чем в одиночку.

Когда ты так взаимодействуешь с системой, координаты перестают быть скучной теорией. Они становятся твоим внутренним компасом для навигации в любом пространстве. От страницы в тетради до цифрового мира.