Четырёхугольники и их свойства

Почему четырёхугольники — это больше, чем просто «четыре линии»

Любой четырёхугольник — это не просто замкнутая фигура с четырьмя сторонами. У него есть внутренняя логика: как связаны стороны, углы и диагонали. Всё подчинено правилам, которые можно увидеть, если посмотреть внимательно.

Когда я впервые нарисовал прямоугольник, мне казалось, что там всё очевидно. Но потом заметил: его диагонали всегда одинаковой длины. Это не совпадение, так получается потому, что противоположные стороны параллельны, а углы прямые. Из этих простых фактов и вытекает равенство диагоналей.

У каждой фигуры свой «характер». У ромба — упрямый: все стороны равны, но углы могут быть и острыми, и тупыми. У трапеции — спокойный: две стороны параллельны, зато за счёт этого она может принимать самые разные формы.

Это не красивые слова, такие знания реально работают. Например, при расчёте конструкций. Однажды я проектировал мостик (для учебной работы), и именно понимание свойств параллелограмма помогло избежать ошибки. Если забыть, что противоположные стороны у него равны и параллельны, модель стать перекошенной. В реальности такая конструкция бы не выдержала.

В 8 классе ты как раз начинаешь видеть, как геометрия переходит от «нарисовать и измерить» к «объяснить и доказать». Четырёхугольники — твой первый серьезный шаг в эту логику. Они лежат в основе формул площадей, помогают решать задачи на доказательство. Даже пригодятся в физике и черчении. Геометрия требует точности, но взамен даёт уверенность. Если рассуждаешь правильно, результат будет верным. Всегда.

Основные виды четырехугольников и их признаки

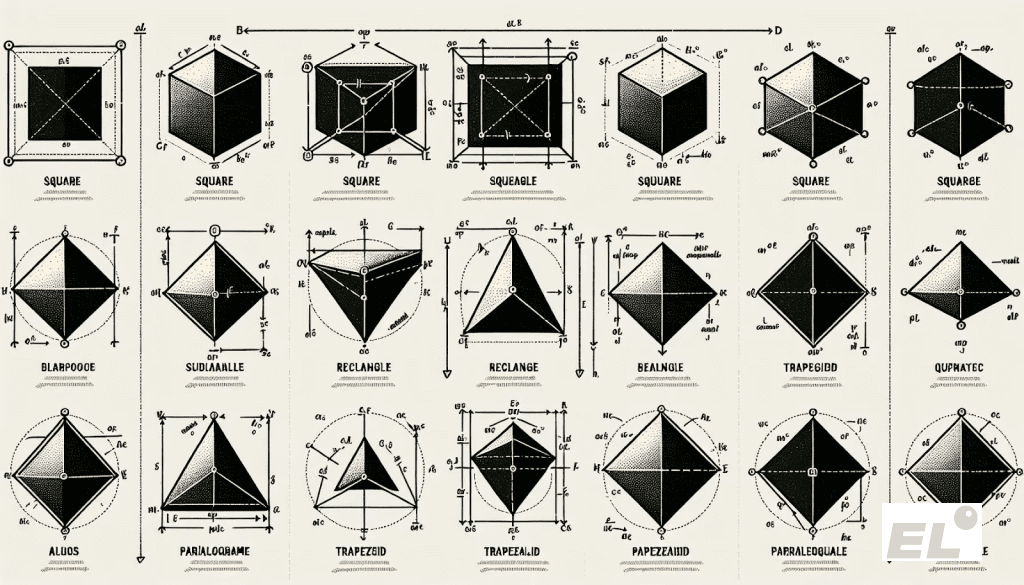
Классификация четырехугольников похожа на семью: у всех общие «корни». Свойства параллельных сторон и углов, но у каждого своя роль и поведение.

Параллелограмм здесь как родоначальник. От него «отпочковываются» три ключевые фигуры:

• Прямоугольник — тот, у кого все углы прямые, а диагонали одинаковой длины.
  
• Ромб — упрямый одиночка: все стороны равны, углы, какие получатся. Зато его диагонали всегда пересекаются под 90° и делят углы пополам.
  
• Квадрат — идеальный гибрид: берёт от прямоугольника прямые углы и равные диагонали, а от ромба равные стороны и перпендикулярные диагонали. Он не просто делит фигуру на треугольники. Делит её на четыре равных прямоугольных треугольника, и это важно при решении задач.

А вот трапеция как двоюродный родственник. У неё только две стороны параллельны. Но и внутри этого «вида» есть свои типы:

• Равнобокая — симметричная, с равными боковыми сторонами и равными углами при каждом основании. Именно такие чаще всего попадались мне в задачах ЕГЭ. Они удобны для построений и доказательств.
  
• Прямоугольная — у неё один угол точно 90°, что упрощает расчёты высот и площадей.

Если ты сейчас в 8 классе, это самое время разобраться в этих «семейных связях». Не зубрить, а понимать, почему одна фигура вытекает из другой. 

Позже, при подготовке к экзаменам, это знание станет фундаментом. И да, хороший курс подготовки для 8 класса по геометрии реально помогает навести порядок в голове. Не просто запомнить, а увидеть логику, которая работает во всех задачах.

Диагонали и углы: невидимые нити симметрии

Если присмотреться, диагонали в четырёхугольниках как внутренние «проводники». Они соединяют противоположные углы и задают фигуру изнутри.

В параллелограмме они пересекаются ровно посередине, каждая делит другую пополам. Это не просто факт для заучивания: именно отсюда вытекает равенство противоположных сторон и симметрия всей фигуры.

У ромба диагонали не только делятся пополам, но и встречаются под прямым углом. Сразу становятся биссектрисами углов. Это свойство часто может спасти в задачах, где просят вычислить угол или доказать перпендикулярность.

У квадрата — полный порядок: диагонали равны, пересекаются под 90°, делят углы его пополам, поворачивают фигуру на 45° относительно сторон. Именно поэтому квадрат так удобен в расчётах, он предсказуем до мелочей.

Когда решаешь задачу, стоит спросить себя: «А что делают диагонали здесь?» Часто именно они открывают путь к решению. Будь то поиск площади, доказательство равенства треугольников или восстановление недостающего элемента.

Мне помогает образ: прямоугольник как экран монитора, четкий и ровный. Ромб — тот же экран, но слегка повернутый в плоскости. Форма изменилась, но сумма углов осталась прежней 360°. Потому что без этого замкнутой фигуры просто не получится. Это как базовый закон равновесия: если один угол «вылезет», то другой должен «подвинуться», иначе система развалится.

Иногда я шучу: квадрат — идеальный гражданин геометрии. Всё у него по правилам: стороны равны, углы прямые, диагонали ведут себя прилично. Мир из таких был бы стабильным, но, честно, скучноватым. 

Хорошо, что есть ромбы с их наклоном к свободе, трапеции с их гибкостью. Они напоминают: порядок важен, но разнообразие делает геометрию живой. И понимание этого, уже половина успеха в решении любой задачи.

Площадь и периметр: как измерить «характер» фигуры

Формулы площадей четырёхугольников не нужно запоминать как заклинания. Их можно вывести, если понимать, как устроена фигура.

У прямоугольника всё прозрачно: S = a * b. Ты просто считаешь, сколько квадратиков со стороной 1 помещается внутри, получаешь произведение длины на ширину.

У ромба формула выглядит загадочнее: S = (d₁ * d₂) / 2. Но стоит разрезать ромб по диагоналям, и он превращается в четыре прямоугольных треугольника. Сложи их правильно, получится прямоугольник со сторонами d₁/2 и d₂/2. Площадь? Та же логика, только теперь через диагонали.

Квадрат — предсказуемый универсал: S = a². Он подходит и под формулу прямоугольника, и под ромбовую. Потому что сочетает их свойства.

А вот трапеция — место, где геометрия показывает изобретательность. Её площадь: S = (a + b) / 2 * h. Это высота, умноженная на длину средней линии (а она как раз равна (a + b) / 2). 

Представь: две одинаковые трапеции, сложенные вместе, дают параллелограмм. Площадь его: (a + b) * h, значит, у одной ровно половина. Когда я сам до этого додумался, действительно почувствовал, будто открыл что-то настоящее.

Эти формулы работают не только в задачах. Ими считают, сколько плитки купить для пола, сколько краски: на стену, или как спроектировать навес.

С периметром всё проще: P = a + b + c + d, просто сумма всех сторон. Здесь часто путают: равные стороны это не значит, равные углы. Например, в ромбе стороны одинаковые, но углы могут быть острыми, тупыми. А в прямоугольнике, наоборот: углы по 90°, а стороны по парам равны.

Основной момент: четырёхугольник гибкий. В отличие от треугольника (где три стороны сразу «фиксируют» форму), у четырёхугольника есть свобода. Можно потянуть за вершину и фигура останется той же «семьи», но площадь изменится. 

Именно эту гибкость используют инженеры: фермы, рамы, мосты. Часто строятся на основе четырёхугольников, чтобы конструкция была легкой, но устойчивой. Понимай не формулы, а почему они такие. Геометрия станет не зубрежкой, а инструментом.

Жизненные параллели и немного философии геометрии

Много лет назад мой преподаватель сказал: «Параллелограмм — это урок баланса». Тогда я усмехнулся, казалось, при чём тут философия к паре параллельных линий? Но сейчас вижу: он был прав.

В параллелограмме всё устроено так, чтобы ничего не завалилось. Противоположные стороны равны и параллельны, каждая повторяет движение другой, сохраняя форму. Диагонали пересекаются ровно посередине, деля пространство честно, без перекосов. Это геометрическая необходимость: без такого равновесия фигура просто не замкнется.

Иногда полезно отвлечься от теорем и спросить: что эта фигура делает? Четырёхугольники тренируют точность, не «примерно параллельно», а именно параллельно. Они развивают умение видеть структуру там, где другие видят хаос.

Посмотри вокруг — особенно в городе. Окна, фасады, плитка на тротуаре, экраны телефонов, рамы солнечных панелей: почти всё построено на четырёхугольниках. Их выбирают не из-за красоты, а потому что они работают: устойчивы, предсказуемы, легко масштабируются.

Геометрия оживает, когда ты начинаешь ее замечать. Тень от здания на асфальте — идеальный прямоугольник. Стропила моста — ромбы и трапеции под нагрузкой. Даже трещина на стекле может напомнить диагонали параллелограмма. Формулы в этом свете становятся языком, на котором мир выстраивает порядок.

Ты учишься видеть логику реальности. И чем лучше чувствуешь эту логику, тем увереннее ориентируешься не только в задачах, но и в жизни.

Как разобраться в свойствах четырехугольников без скуки

Мой совет: начинай с рисунка. Возьми лист, нарисуй разные четырёхугольники: параллелограмм, ромб, трапецию, квадрат. Проведи диагонали, отметь углы, подпиши равные стороны. Не стремись сразу к идеальной точности, важно увидеть связи. Чем больше строишь, тем быстрее глаз начинает замечать закономерности без подсказок.

Когда картинка в голове стала чёткой, переходи к задачам. Не заучивай формулы наизусть, попробуй вывести их сам. Например, почему площадь ромба равна половине произведения диагоналей? Разрежь его мысленно и всё станет ясно. Такое знание не забывается.

Полезный приём: проговаривай вслух, как устроена фигура. Объясняй, почему диагонали делятся пополам или почему углы при основании трапеции равны. Даже если рядом никого нет, говори себе, будто помогаешь другу. Я так делал на старших курсах, и это реально укрепляло понимание.

Ошибки — не провал, а часть процесса. Если линия пошла не туда или вывод не сошёлся, это сигнал: где-то пропущена связь. Я часто слышу: «Ничего не получается!» — и отвечаю: «Хорошо. Значит, ты ещё не видишь внутреннюю структуру. Но скоро увидишь». Через месяц ученик возвращается и улыбается. Фигура перестала быть набором букв и линий. Она стала живой.

Четырехугольники могут стать увлекательным миром, если смотреть на них с любопытством и давать себе время разобраться. Терпение здесь не добродетель, а рабочий инструмент.